Introducción a Matlab

Introducción a Matlab

por Ángel Garcimartín
Departamento de Física y Matemática Aplicada

Véase también:Introducción a la programación con Matlab

Matlab es un programa interactivo para cálculo numérico y tratamiento de datos. Contiene muchas herramientas y utilidades que permiten además diversas funcionalidades, como la presentación gráfica en 2 y 3 dimensiones. Esos útiles están agrupados en "paquetes" (toolboxes). A Matlab se le pueden añadir paquetes especializados para algunas tareas (por ejemplo, para tratamiento de imágenes). Trabajar con Matlab comporta aprender un lenguaje simple. En esta introducción se explican los elementos básicos de este lenguaje.

Matlab es un programa command-driven, es decir, que se introducen las órdenes escribiéndolas una a una a continuación del símbolo » (prompt) que aparece en una interfaz de usuario (una ventana). Esta introducción contiene ejemplos que se pueden escribir directamente en la línea de comandos de Matlab. Para distinguir esos comandos, junto con la respuesta del programa, se emplean un tipo de letra diferente:

»2+2

ans =

4

Una manera de seguir esta introducción consiste en abrir Matlab en otra ventana, e ir copiando y pegando el comando a continuación del símbolo >>.

Para más información, se puede consultar el folleto "Getting Started with Matlab" o el manual de usuario (que están en la biblioteca). También puede consultarse la ayuda en línea, como se explica más adelante. O conectarse al servidor Web de Mathworks, la empresa que comercializa Matlab, donde pueden encontrarse -por ejemplo- programas que han escrito otros usuarios de Matlab.

Este documento contiene los siguientes apartados:

"Scripts"
Cálculo simbólico
Sugerencias

Para saber más: una página Web de introducción a la programación con Matlab.

Comandos básicos

En esta sección se explica cómo usar Matlab a modo de calculadora.

Empecemos con algo sencillo: las operaciones matemáticas elementales.

» x=2+3

x =

5

Si no se asigna el resultado a ninguna variable, Matlab lo asigna por defecto a la variable ans (answer):

» 2+3

ans =

5

Para saber cuál es el valor asignado a una determinada variable, basta introducir el nombre de la variable:

» x

x =

5

La notación para las operaciones matemáticas elementales es la siguiente:

^	exponenciación
*	multiplicación
/	división
+	suma
-	resta

El orden en que se realizan las operaciones de una línea es el siguiente: primero, la exponenciación; luego, las multiplicaciones y divisiones; y finalmente, las sumas y las restas. Si se quiere forzar un determinado orden, se deben utilizar paréntesis, que se evalúan siempre al principio. Por ejemplo, para hallar dos entre tres,

» 2/2+1

ans =

2

(en efecto: primero se calcula 2/2 y luego se suma 1).

» 2/(2+1)

ans =

0.6667

Primero se calcula el paréntesis (2+1) y luego se realiza la división.

Dos observaciones. El punto decimal es . (no una coma). Y en Matlab, las mayúsculas y las minúsculas son distintas. Es decir, X es una variable diferente de x.

En Matlab están también definidas algunas funciones elementales. Las funciones, en Matlab, se escriben introduciendo el argumento entre paréntesis a continuación del nombre de la función, sin dejar espacios. Por ejemplo:

» y=exp(0)

y =

1

(la función exp es la exponencial). He aquí una tabla con algunas funciones elementales:

`sin`	seno
`cos`	coseno
`tan`	tangente
`sec`	secante
`csc`	cosecante
`cot`	cotangente
`exp`	exponencial
`log`	logaritmo natural
`sqrt`	raíz cuadrada
`abs`	valor absoluto

Para obtener las funciones trigonométricas inversas, basta añadir una a delante del nombre. Y para las funciones hiperbólicas, una h al final. Por ejemplo, atanh(x) es el arcotangente hiperbólico de x:

» z=atanh(2)

z =

0.5493 + 1.5708i

(z es un número complejo).

Ayuda en línea

Cómo obtener información sobre los comandos de Matlab.

Este documento es tan sólo una introducción -muy resumida- del lenguaje y del manejo de Matlab. Antes de seguir, es conveniente indicar cómo puede obtenerse más información sobre cualquier detalle referente a Matlab. Por supuesto, siempre se pueden consultar los manuales: hay un ejemplar en las salas del C.T.I. y otro en la biblioteca, que puede obtenerse en préstamo por un día.

Además, desde dentro de Matlab pueden obtenerse explicaciones sobre un tema particular. Hay varios métodos.

El comando help. Para obtener información sobre una determinada función, basta teclear desde la línea de comandos help seguido del nombre de la función. Por ejemplo:

» help round

ROUND Round towards nearest integer.

ROUND(X) rounds the elements of X to the nearest integers.

See also FLOOR, CEIL, FIX.

Si se escribe sólo help, se obtiene un índice de temas. También puede obtenerse información sobre uno de los temas de esa lista: así, help elfun proporciona información sobre las funciones matemáticas elementales.

La ventana de ayuda. Puede llamarse tecleando helpwin o bien escogiendo del menú Help el ítem Help Window. Se obtiene una ventana nueva, y haciendo doble click con el ratón sobre un capítulo se pasa a un elenco de los ítems contenidos, que a su vez pueden escogerse para una explicación más detallada. Con los botones Back y Forward se navega hacia atrás o hacia adelante. También puede escribirse directamente en la zona superior izquierda el nombre del comando deseado: por ejemplo, para buscar información sobre sqrt ...

En la barra See also aparecen comandos relacionados. La información es la misma que la obtenida con el comando help, pero con la comodidad de presentarse en una ventana aparte en vez de en la línea de comandos.

La ayuda interactiva. Se obtiene escogiendo del menú Help el ítem Help Desk, o tecleando helpdesk en la barra de comandos. Se lanza el navegador y se obtiene un documento de inicio con un índice de temas en hipertexto donde están los manuales y otras utilidades, como un buscador. Para leer el manual, se necesita el programa Acrobat Reader.

La información que se obtiene es mucho más completa que en los otros dos casos, lo cual puede resultar inconveniente si uno desea simplemente, por poner un caso, conocer la sintaxis de una función.

Una introducción a Matlab más rigurosa, extensa y comprensiva que este documento puede encontrarse en el epígrafe "Getting Started" del Help Desk.

El entorno Matlab

Para desenvolverse en la interfaz de usuario, llevar la cuenta de las variables, ...

Edición de la línea de comandos. Con las flechas del teclado se pueden recuperar las órdenes anteriores, sin tener que volver a teclearlas. Así, en el caso de una equivocación en un comando complicado

» d2_f=(y2-2*y1+y3)/deltax^2)

??? -2*y1+y3)/deltax^2)

|

Missing operator, comma, or semi-colon.

en vez de volver a teclear todo, puede recuperarse la instrucción pulsando la tecla "flecha hacia arriba", desplazarse hasta el error (falta un paréntesis) con la flecha hacia a la izquierda, y arreglarlo:
» d2_f=(y2-2*y1+y3)/(deltax^2)

En ocasiones, es interesante no presentar el resultado en la pantalla (por ejemplo, cuando se trata de una lista de datos muy larga). Eso se consigue poniendo un punto y coma al final de la instrucción.

» y=sqrt(4);

El resultado no aparece, pero sin embargo el cálculo se ha realizado:

» y

y =

2

El comando who indica las variables con las que se está trabajando:

» who

Your variables are:

Fy f indice n_punt t_m

delta_f f_max manchas t y

Comandos relacionados con el sistema operativo:

`pwd`	Present working directory (directorio de trabajo actual)
`cd`	cambiar de directorio
`dir`	listado de los ficheros del directorio actual

Estos comandos son muy similares a los análogos de MS-DOS o UNIX.

Guardar y cargar ficheros de datos. Se emplean los comandos save y load, respectivamente.

para guardar datos: save [nombre del fichero] [variable] -ascii

para recuperar datos: load [nombre del fichero] [variable] -ascii

Por ejemplo: con estas dos órdenes

» cd a:

» save toto.dat y -ascii

se cambia el directorio de trabajo a a:\ y se guarda allí el contenido de la variable y en el fichero toto.dat con formato texto (por eso se pone -ascii).

Vectores y matrices

La "especialidad" de Matlab es el manejo de matrices: Matlab son las siglas de Matrix Laboratory.

Un vector se define introduciendo los componentes, separados por espacios o por comas, entre corchetes:

» v=[sqrt(3) 0 -2]

v =

1.7321 0 -2.0000

Para definir un vector columna, se separan las filas por puntos y comas:

» w=[1;0;1/3]

w =

1.0000

0

0.3333

La operación transponer (cambiar filas por columnas) se designa por el apóstrofe:

» w'

ans =

1.0000 0 0.3333

Las operaciones matemáticas elementales pueden aplicarse a los vectores:

» v*w

ans =

1.0654

» v+w'

ans =

2.7321 0 -1.6667

Para crear un vector de componentes equiespaciados se emplean los dos puntos:

» x=4:2:10

x =

4 6 8 10

(los componentes de x van desde 4 de 2 en 2 hasta 10).

Para introducir matrices, se separa cada fila con un punto y coma:

» M = [1 2 3 ;4 5 6 ;7 8 9]

M =

1 2 3

4 5 6

7 8 9

Para referirse a un elemento de la matriz se hace así:

» M(3,1)

ans =

7

Para referirse a toda una fila o a toda una columna se emplean los dos puntos:

» v1=M(:,2)

v1 =

2

5

8

(v1 es la segunda columna de M).

Con las matrices también funcionan las operaciones matemáticas elementales. Así

» M^2

ans =

30 36 42

66 81 96

102 126 150

Si se quiere operar en los elementos de la matriz, uno por uno, se pone un punto antes del operador. Si se quiere elevar al cuadrado cada uno de los elementos de M, entonces

» M.^2

ans =

1 4 9

16 25 36

49 64 81

Algunas funciones definidas sobre matrices:

`det`	determinante
`inv`	matriz inversa
`poly`	polinomio característico
`'`	transpuesta

(Para más información: help elmat)

Poliniomios

En Matlab los polinomios se representan por vectores cuyas componentes son los coeficientes del polinomio.

Sea

Este polinomio se representa por un vector p

» p=[1 -3 +2]

p =

1 -3 2

Para hallar las raíces del polinomio, se hace

» roots(p)

ans =

2

1

y si se quiere hallar el valor de P(x) para un determinado valor de x (por ejemplo, para x=0)

» polyval(p,0)

ans =

2

Gráficos

Cómo presentar datos con Matlab.

Las posibilidades de Matlab son muy grandes. Se indica a continuación cómo realizar gráficos sencillos. Para más información, o para conocer la versatilidad de Matlab: capítulo Handle Graphics Object del Help Desk, el manual Using MATLAB Graphics o la ayuda en línea help graph2d.

Veamos cómo se puede representar la función seno entre 0 y 10. Para empezar creemos una variable x que vaya de cero a 10:

» x=0:0.1:10;

y a continuación, calculemos sin(x) almacenando el resultado en la variable y:

» y=sin(x);

Para trazar el gráfico, se emplea la función plot:

» plot(x,y)

y se obtiene en otra ventana el gráfico:

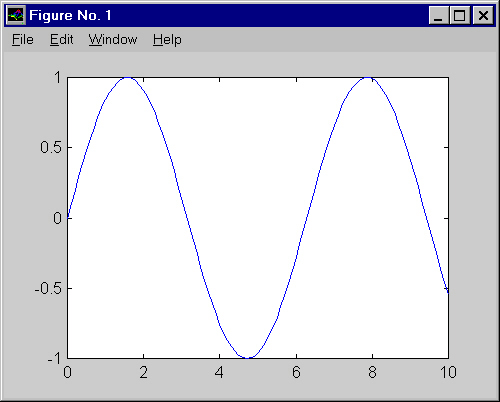
Entre los muchos comandos que se pueden utilizar para modificar los gráficos, es muy útil el empleado para cambiar la escala de los ejes. La orden es

axis([x1 x2 y1 y2])

donde x1, x2 son los límites inferior y superior del eje x, e y1 e y2 los del eje y.

Para representar unos datos con símbolos de colores, se añade al comando plot, entre apóstrofes, la especificación. Vamos a crear una variable con dos filas que contenga los números del 1 al 10 en la primera fila, y el doble de esos números en la segunda, y dibujarlos con puntos rojos:

» x(1,:)=0:10;

» x(2,:)=2*x(1,:);

» x

x =

0 1 2 3 4 5 6 7 8 9 10

0 2 4 6 8 10 12 14 16 18 20

» plot(x(1,:),x(2,:),'ro')

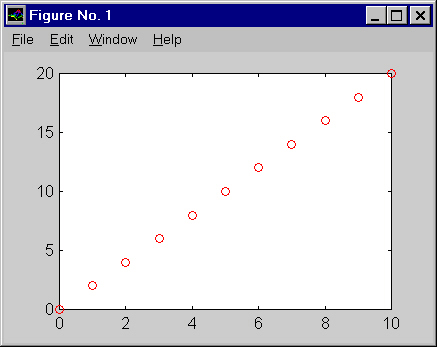
(para ver las especificaciones posibles, teclear help plot. Por ejemplo, 'ro' establece un gráfico de color rojo: r y de puntos: o.) Si no se indica nada, el gráfico se traza con una línea azul.

Otras funciones muy útiles: grid, que traza una cuadrícula, xlabel('títulox')eylabel('títuloy'), que sirven para poner un título en los ejes.

Para imprimir una figura, basta seleccionar print del menú de la figura.

"Scripts"

Archivos de órdenes: programar en Matlab.

Realizar un programa en Matlab es fácil. Basta abrir un editor de texto (como el Bloc de Notas de Windows) y escribir los comandos uno a continuación de otro. Luego ese fichero de texto debe guardarse con la extensión .m, y a eso se le llama un script:

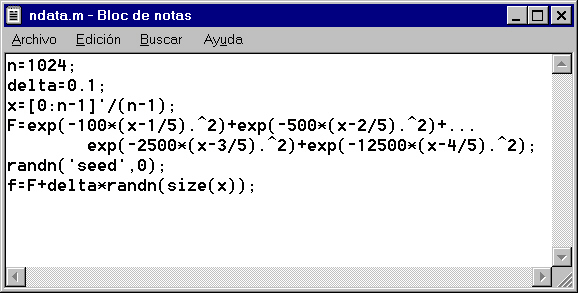
Una vez guardado el fichero (en el ejemplo, ndata.m) en el directorio actual, desde la línea de comandos de Matlab basta escribir ndata para que se ejecute el programa.

A partir de aquí, se abren las posibilidades de la programación con un lenguaje sencillo. Puede verse una página Web de introducción a la programación aquí.

Cálculo simbólico

Matemáticas en el ordenador.

Hasta ahora, las operaciones que se han mostrado se han realizado con números. El toolbox de cálculo simbólico permite realizar cálculos abstractos:

» diff('sin(x)')

ans =

cos(x)

Las expresiones simbólicas se introducen entre apóstrofes.

A continuación se da una tabla con algunas funciones de este toolbox, junto con un ejemplo de cada una:

`diff`	derivada	`diff('sin(x)')`
`int`	integral	`int('x^2')`
`solve`	resolución de ecuaciones	`solve('x^2-3*x+2=0')`
`ezplot`	gráficos	`ezplot('exp(x)')`

Evidentemente, las expresiones pueden ser todo lo complicadas que se quiera ...

» solve('x=cos(x)')

ans =

.73908513321516064165531208767387

» int('(x^4+4*x^3+11*x^2+12*x+8)/((x^2+2*x+3)^2*(x+1))')

ans =

log(x+1)+1/8*(-4*x-8)/(x^2+2*x+3)-1/4*2^(1/2)*atan(1/4*(2*x+2)*2^(1/2))

Se agradece cualquier sugerencia sobre este documento. Puede enviarse un mensaje por correo electrónico a elm