Dynamics of open Bose-Einstein condensates

Predicted theoretically in the twenties of last century, Bose-Einstein condensate (BEC for short), is a new state of matter where bosons are cooled to temperatures very near to absolute zero (0 K or −273.15 °C). Under such supercooled conditions, a large fraction of the atoms collapse into the lowest quantum state of the external potential, at which point quantum effects become apparent on a macroscopic scale. 

Experimental verifications were achieved seventy years later when the first gaseous condensate was produced by Eric Cornell and Carl Wieman in 1995 at the University of Colorado at Boulder NIST-JILA lab, using a gas of rubidium atoms cooled to 170 nanokelvin (nK).
Eric Cornell, Carl Wieman and Wolfgang Ketterle at MIT were awarded the 2001 Nobel Prize in Physics in Stockholm, Sweden.
On the side figure is shown the velocity-distribution data of a gas of rubidium atoms, confirming the discovery of a new phase of matter, the Bose–Einstein condensate. Left: just before the appearance of the Bose–Einstein condensate. Center: just after the appearance of the condensate. Right: after further evaporation, leaving a sample of nearly pure condensate.
 image not available
 

Compared to more commonly-encountered states of matter, Bose–Einstein condensates are extremely fragile. The slightest interaction with the outside world can be enough to warm them past the condensation threshold, forming a normal gas and losing their interesting properties.

In 1999, together with F.T. Arecchi and L. Castellanos, we have studied how an atomic Bose Einstein condensate couples to a source of uncondensed atoms at the same temperature and to a sink (modelling the extraction towards an atom laser). The idealized description of BEC in terms of a Gross–Pitaevsky equation no longer
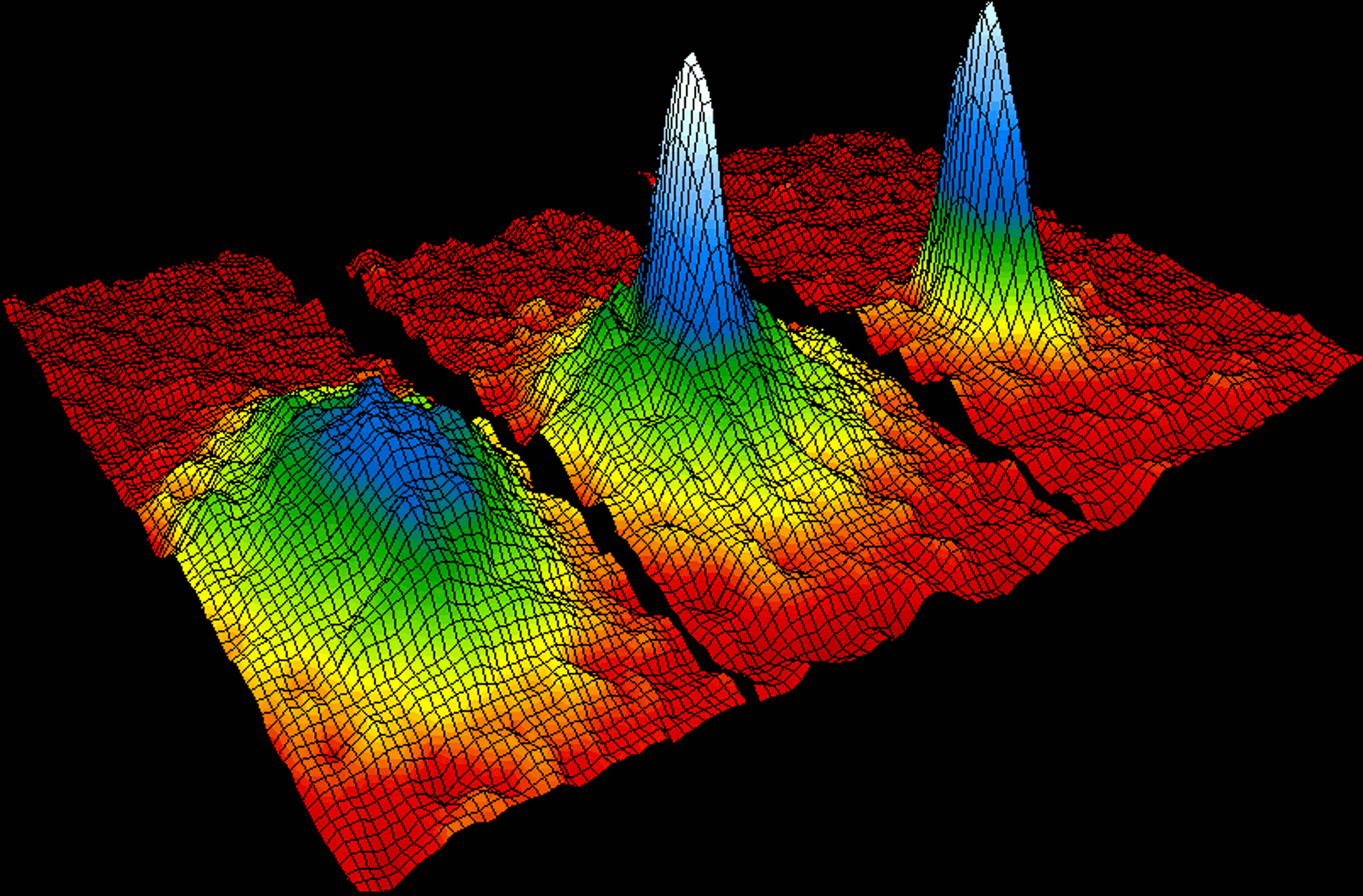
holds. Under suitable physical assumptions we show that the dissipative BEC obeys a Complex Ginzburg Landau equation and for some parameter range it undergoes a space time patterning (as shown below in the case of 7Li). As a consequence, the density of BEC atoms within the trap displays non trivial space time correlations, which can be detected by monitoring the density profile of the outgoing atom laser. The patterning condition requires a negative scattering length, as e.g. in 7Li. In such a case we expect a many domain collapsed regime, rather than a single one as reported for a closed BEC.

More details of the research can be found in the following article published in 2000.

Here is shown a movie (animated GIF) corresponding to the snapshots shown below (open BEC in the case of 7Li).
In the following pictures are depicted the density of the open condensate when time evolves.

image not available image not available
t=0 t=10
image not available image not available
t=500 t=1000